deeplearning.ai深度学习笔记(Course4 Week1):Foundations of Convolutional Neural Networks
本周讲述了CNN的基础。从边界检测引入卷积运算,并将2D卷积运算延伸到3D中的multi-filter,最后以LeNet-5架构为例整体介绍了CNN。
1- Convolutional Neural Networks
1.1- Computer Vision
计算机视觉(computer vision)是因deep learing而快速发展的领域之一,并促进了自动驾驶、人脸识别等应用的发展以及更多的全新应用(而这些在几年前还是不可能的),计算机视觉的发展也为其他领域如语音识别提供了思路。
计算机视觉的例子:
- Image classification
- Object detection
- Neural Style transfer
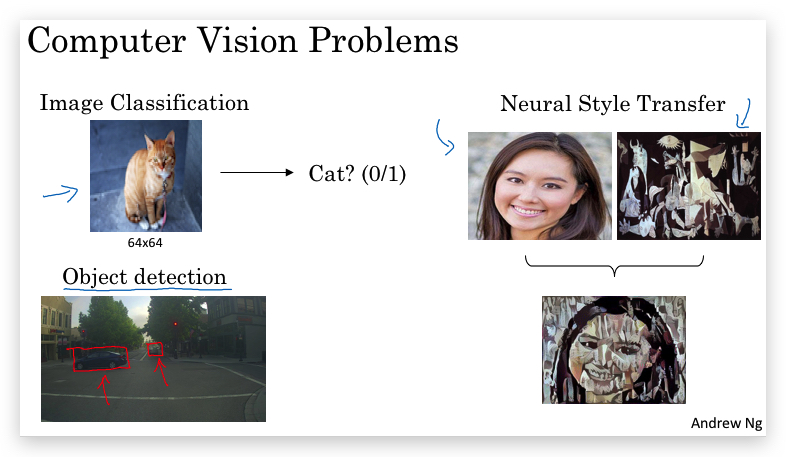
计算机视觉的一个挑战:图片数据转换的特征向量太大。比如一张1000x1000像素的图片,转化成向量则有1000x1000x3=3百万个输入属性。这将导致
- Neural Network的结构十分复杂,参数很多,容易产生过拟合;
- 庞大的计算量。
这正是卷积神经网络(convolutional neural network, CNN)要解决的。
1.2- Edge Detection Example
Convolution opteration(卷积运算)是convolutional neural network的重要基石之一。
Edge Detection分为:
- vertical edges
- horizontal edges
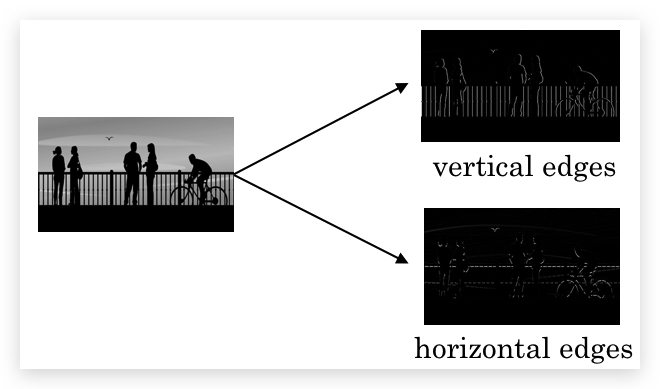
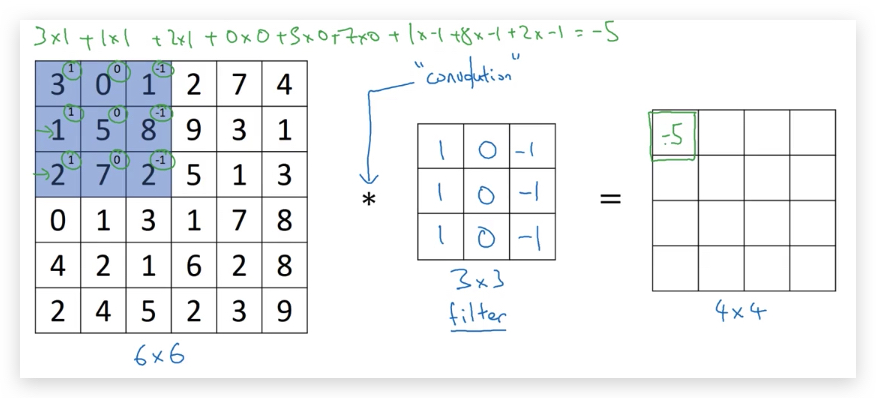
举例:Vertical edge detection vertical edge detection可以用卷积运算实现。比如检测一张6x6像素的灰度图片的vertical edge,设计一个3x3的矩阵(称之为filter或kernel),让原始图片和filter矩阵做卷积运算(convolution),得到一个4x4的图片。 具体的做法是,将filter矩阵贴到原始矩阵上(从左到右从上到下),依次可以贴出4x4种情况。让原始矩阵与filter重合的部分做element wise的乘积运算再求和,所得的值作为4x4矩阵对应元素的值。如下图是第一个元素的计算方法,以此类推。
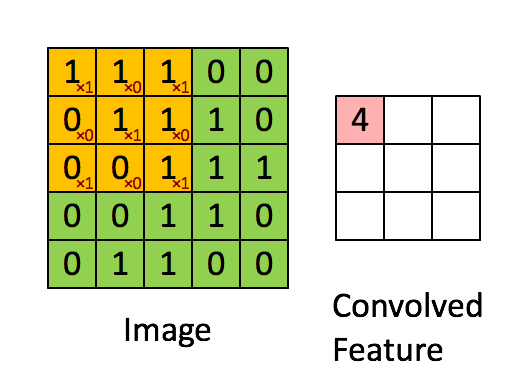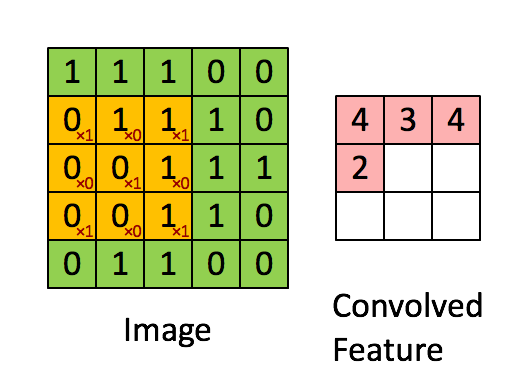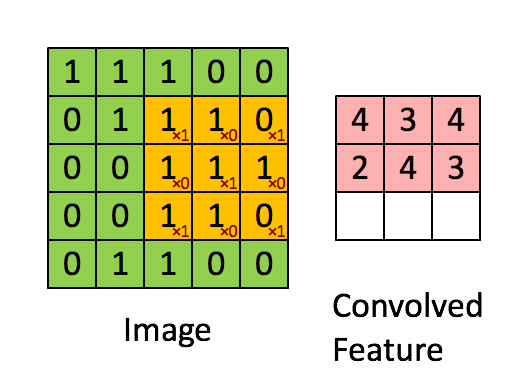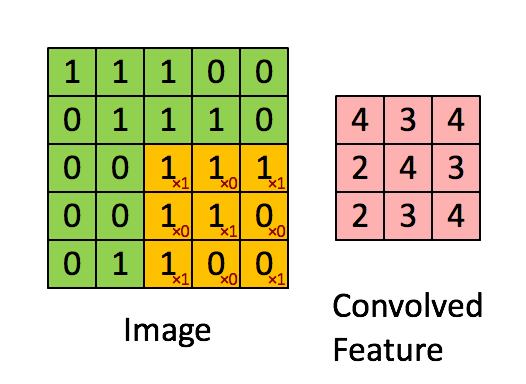
下面是一个动图展示了卷积操作:
使用卷积做边缘检测的解释:
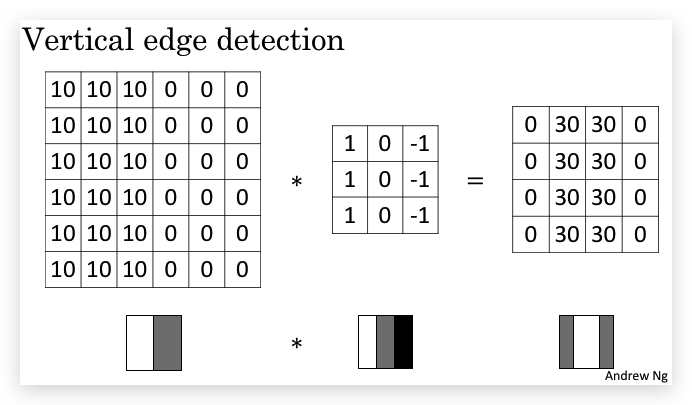
如上图,通过filter卷积运算后,右边的矩阵会出现一条中间的空白,代表了边缘所在的位置。
我的理解:filter矩阵很有意思,它是左右堆成且只相反,如果不是边缘(即像素值比较均匀),经过filter运算后的点(相当于做了加权平均)基本被抵消为0。如果filte在边缘处运算,会造成明显的不平衡,即显示出边缘所在。
这里的卷积,本质上是图片的某个区域与filter的内积,而内积反应的是相似性。所以用一个1,0,-1的filter找到的就是和气相似的区域,即垂直边缘。
关于卷积,参考资料:卷积的理解
1.3- More Edge Detection
- 亮到暗与暗到亮
以vertical edge detection为例,亮到暗与暗到亮会形成两种不同的检测结果,如下图使用相同的filter,分别得到30和-30的边界:
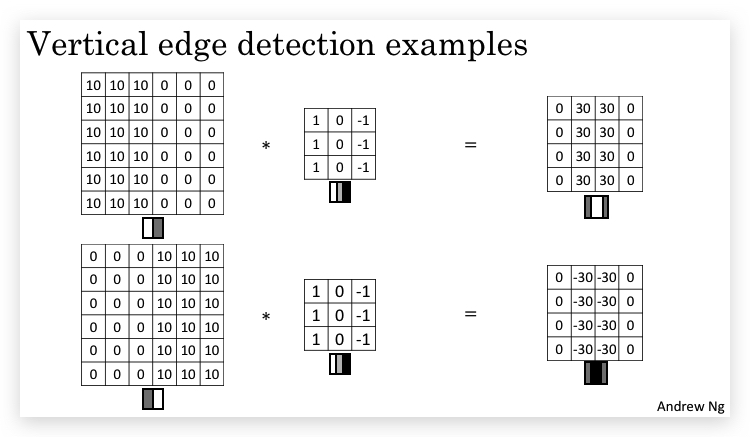
因此,根据生成的边界的正负,可以得知边界的类型。
- horizontal edge detection 类似,将filter做一个转置,即得到了horizontal edge detection的filter
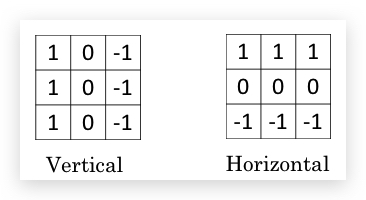
一个稍复杂的horizontal edge detection,左边是由亮到暗,右边是由暗到亮:
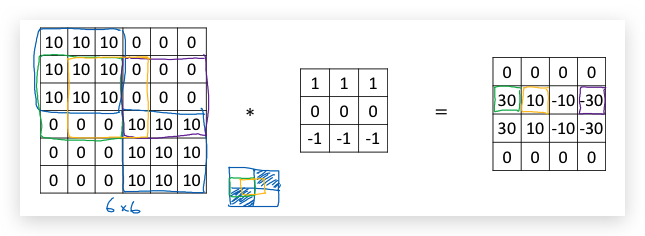
通过正负,可以得知30表示左边的水平边界是positive edge,即亮到暗,而-30则表示右半部分则是negative edge,即暗到亮。
- filter的选择 除了上面的-1,0,1的filter外,还有其他类型的filter,它们加强了中心点的权重,使得算法更健壮,比如:
- Sobel fitler
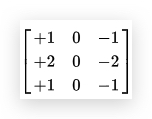
- Scharr filter
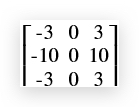
- 算法学习filter 与人工设置filter对应,也可以通过算法训练出一个filter,即将filter看成参数,使用反向传播算法学习(后续会介绍)。而且不仅限于vertical和horizontal,算法还可以学习出各种角度的filter。
1.4- Padding
为了构建deep neural network,对基本卷积操作的一个改进就是padding。
问题:通过filter卷积运算后的矩阵维度会比原矩阵变小了,比如一个6x6的矩阵经过3x3的filter卷积运算后,只有4x4的维度了。一般的,对于一个\(n\times n\)的矩阵,经过\(f\times f\)的filter运算后是\((n-f+1)\times (n-f+1)\)维。这造成两个缺陷:
- 图片运算后被缩小了(shrink output),如果neural network层数较多,可能会缩小的很严重,因为每一层都会缩一次。
- 边界上的像素被运算的次数要小于中心的像素,比如左上角的像素只会参与一次卷积运算。丢失了图片边缘的信息。
解决的办法是padding,即在原始矩阵围一圈(通常用0填充)。比如对于3x3的fitler,把原始图片矩阵上下左右各padding一个单位(padding=1),一个6x6的矩阵padding后变成了8x8的矩阵,卷积后还是6x6的矩阵。
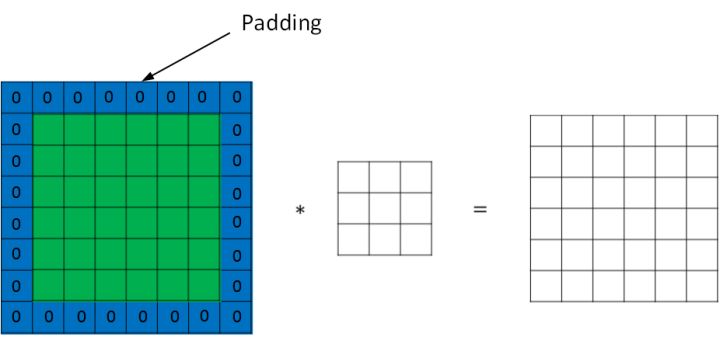 (图片来源:http://kyonhuang.top/Andrew-Ng-Deep-Learning-notes/#/Convolutional_Neural_Networks/%E5%8D%B7%E7%A7%AF%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C)
(图片来源:http://kyonhuang.top/Andrew-Ng-Deep-Learning-notes/#/Convolutional_Neural_Networks/%E5%8D%B7%E7%A7%AF%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C)
考虑到是否padding,卷积运算分为了两种:
- Valid convolutions 即没有padding
- Same convolutions 有padding,使得输出矩阵和输入矩阵保持相同的大小
在计算机视觉领域,filter的大小f通常取奇数通常取奇数,为了保证输出矩阵大小不变,padding的大小则是:\(p=\frac{f-1}{2}\)
1.5- Strided Convolutions
前面的例子,在做卷积的时候,filter每次移动的距离是1,而Stride convolution允许移动的距离大于1,比如下图设置的stride是2:
结果矩阵中,第一个元素的计算是取左上角9个元素(图中蓝色部分)和filter运算,得到91
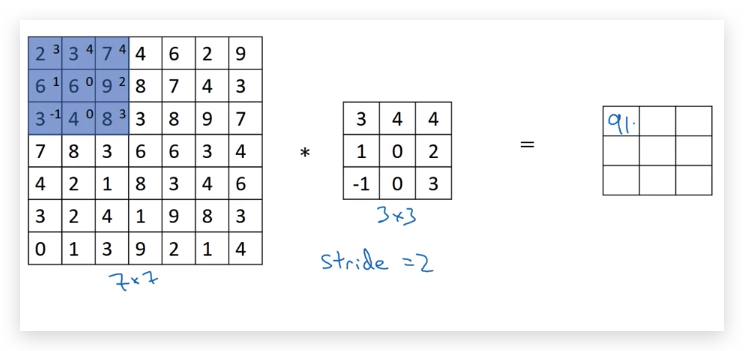
然后直接向右移动两格(图中蓝色部分)做卷积运算,得到第二个元素100:
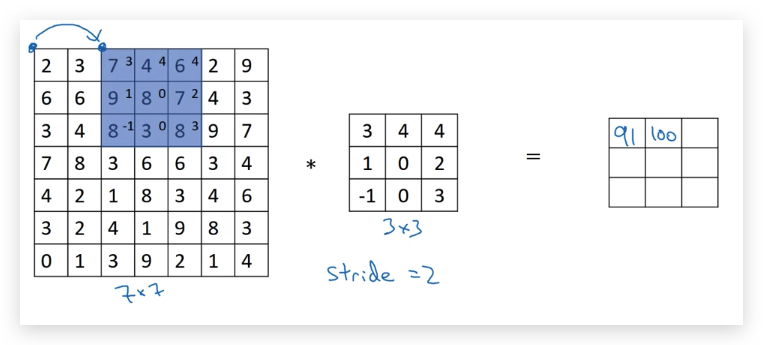
以此类推:
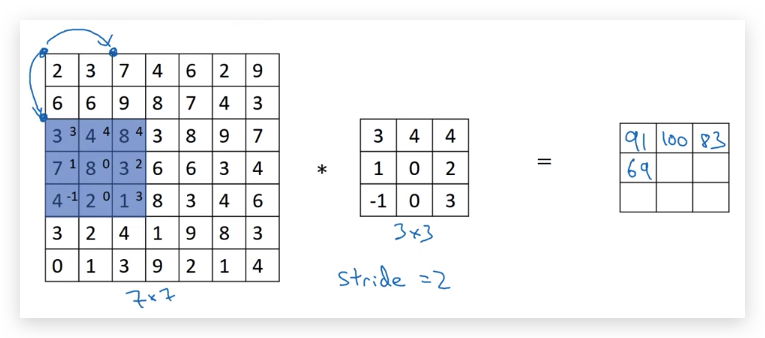
很显然,结果矩阵比原矩阵要小,变成了只有3x3的矩阵。
如果原矩阵大小是\(n \times n \),padding是\(p\),filter矩阵大小是\(f \times f\),stride是\(s\),则可以计算结果矩阵的大小是:\(\biggl\lfloor \frac{n+2p-f}{s}+1 \biggr\rfloor \times \biggl\lfloor \frac{n+2p-f}{s}+1 \biggr\rfloor\)
关于卷积和互相关(cross-correlation)的说明: 严格来说,前面介绍的卷积和数学上的卷积定义有所差别。数学上的卷积,在乘积求和之前要先把filter矩阵沿着反斜对角线旋转一下,如下图:
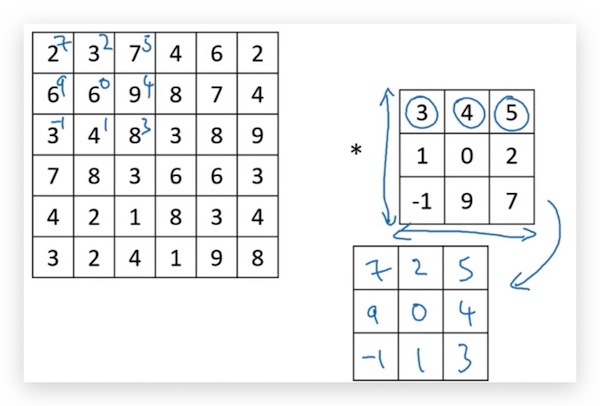
做旋转的好处是,可以使得卷积操作满足结合律。
但在machine learing语境中,由于filter基本是垂直或水平的,旋转与否影响不大,故习惯上还是将cross-correlation称作convolution。
参考资料:卷积与互相关的一点探讨
1.6- Convolutions Over Volume
前面介绍的卷积都是应用在二维灰度图片上,现在将卷积应用于三维上(比如RGB图片)
- RGB图片卷积运算的例子:
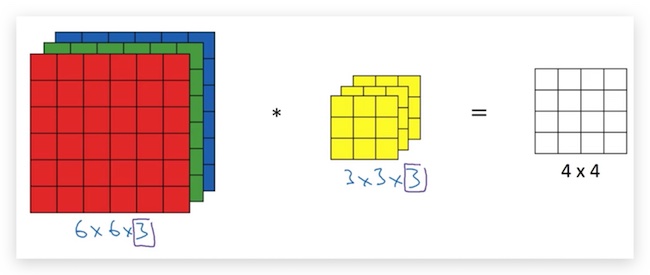
RGB图片需要用三个矩阵叠加,分别表示RGB三种颜色。原始图片的size是6x6x3,图片的本身的尺寸6x6称作height和width,而叠加的层数成为channel(这里RGB构成的channel为3),对应的filter也需要三层,即filter的channel要与原始图片的channel一样。
运算规则是,RGB的每一个channel和filter每一个channel先做卷积,然后将每个channel的卷积加总,作为结果矩阵的对应元素值,如下图:
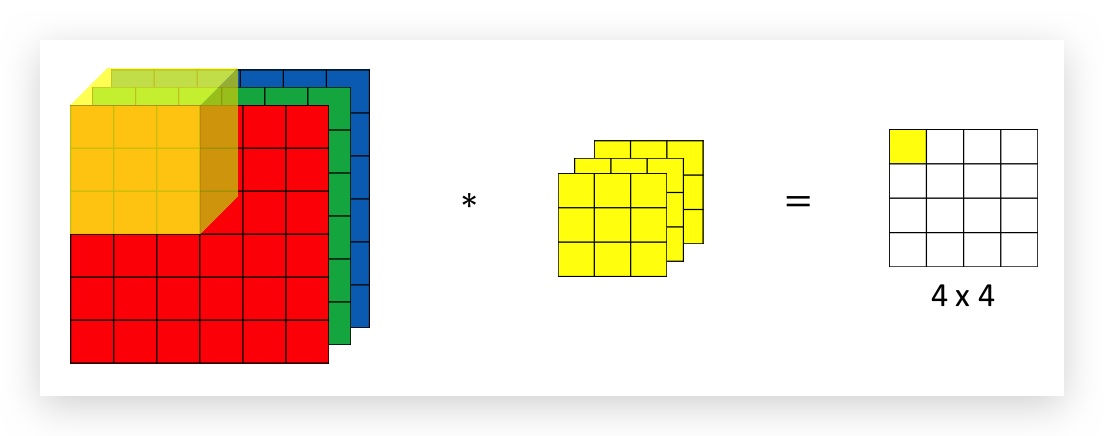
依次类推:
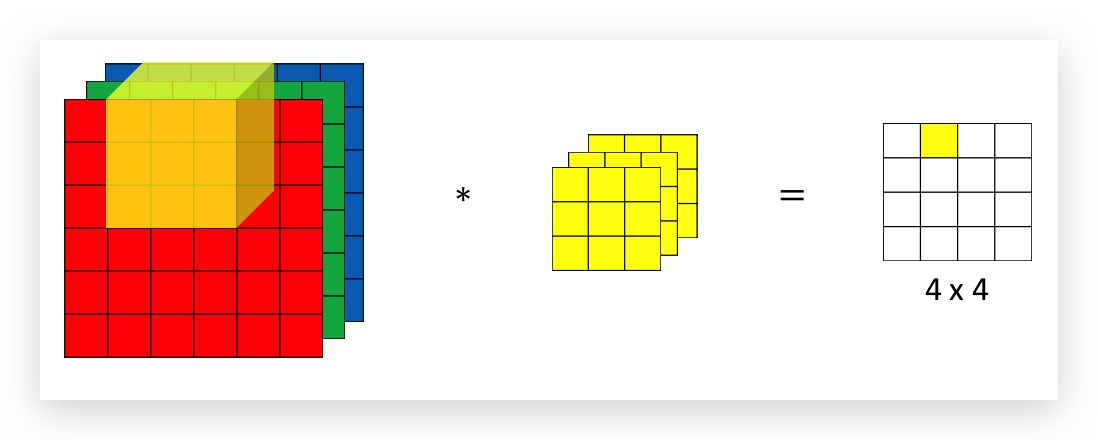
如果仅关注一种颜色(比如红色)的边界,则可以将filter中绿色和蓝色层的矩阵设置为全零矩阵。如果RGB三种颜色的边界都考虑,则将filter三层设置为一样的矩阵。
- Multi filters
Multi filters是构建CNN的重要思想。如果我们不只想检测水平和垂直边界,比如还想检测45度,甚至70度的边界呢?换句话说,如何同时应用多个filter呢?
可以这样思考,图片分别应用了两个filter,比如一个是水平filter、一个是垂直filter,分别得到两个目标矩阵,都是一层channel;然后这两个矩阵叠一起就变成了一个2层channel的矩阵,如下图:
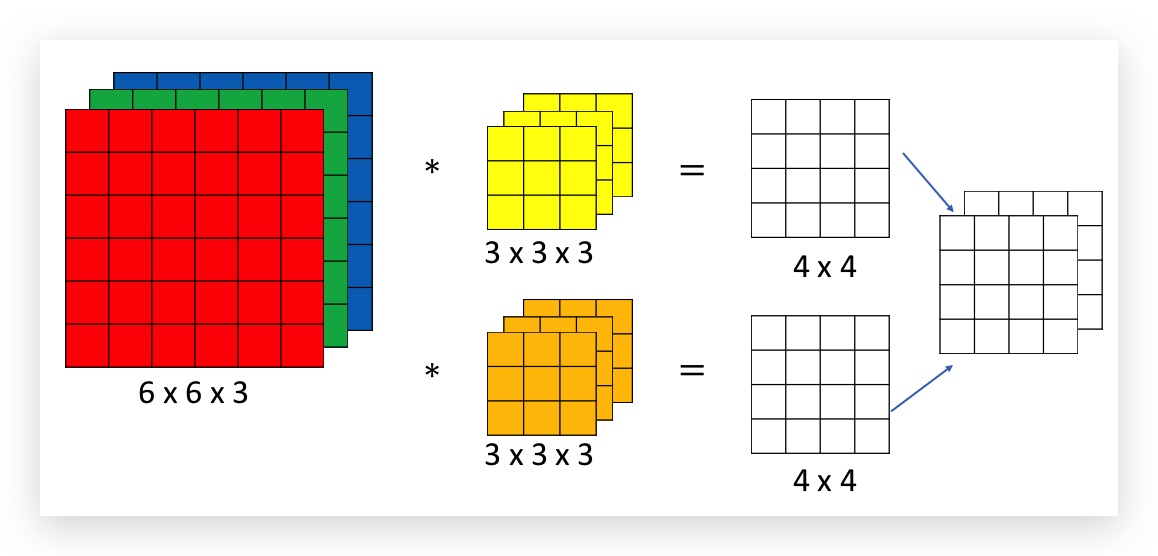
输出矩阵的channel数则与应用的filter的个数一样。
multi-filter使得算法可以学习出多种feature。如果把一个filter整体看成基本神经网络中的参数w的话,那么multi-filter就相当于多个w。在基本神经网络中,我们也有W的行数和输出矩阵的行数一样,这一点类似filter个数和输出矩阵的channel的关系。
另外一张RGB图片,可以认为天然的被拆分成3个feature。
综上所述,你可以同时应用多个filter,并且每个filter又有多个channel,在这个基础上就可以实现CNN了。
1.7- One Layer of a Convolutional Network
一个单层的卷积神经网络例子如下:
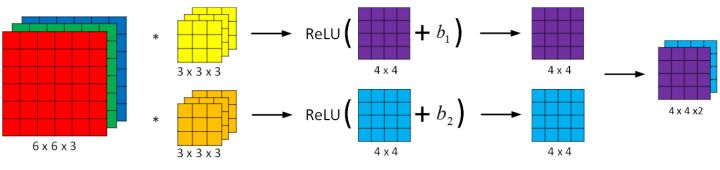 (图片来源:http://kyonhuang.top/Andrew-Ng-Deep-Learning-notes/#/Convolutional_Neural_Networks/%E5%8D%B7%E7%A7%AF%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C?id=%E5%8D%95%E5%B1%82%E5%8D%B7%E7%A7%AF%E7%BD%91%E7%BB%9C)
(图片来源:http://kyonhuang.top/Andrew-Ng-Deep-Learning-notes/#/Convolutional_Neural_Networks/%E5%8D%B7%E7%A7%AF%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C?id=%E5%8D%95%E5%B1%82%E5%8D%B7%E7%A7%AF%E7%BD%91%E7%BB%9C)
输入一张RGB图片,经过两个filter得到卷积,在卷积结果上加上偏移b1和b2,再应用activation function,得到输出层。
下面是动画演示,很形象:
对比基本的Neural Network,可以发现filter类似于参数\(W^{[1]}\)。
而卷积运算在加上后的b,即,也可以看做是原图像和filter上每个元素的线性组合,这也类似于基本Neural Network中计算z的过程:\(z^{[1]}=W^{[1]}a^{[0]} + b^{[1]}\)
每一个channel可以理解为普通NN中的一个实数w。
参数个数 问:如果一个layer有10个filter,每个filter是3x3x3,本层一共有多少参数? 答:一个filter有27个参数,再加上一个bias参数b,一个filter对应28个参数,10个filter一共280个参数。
与基本NN不同,CNN的参数个数并不随输入增大(共享参数的原因,后面会介绍),无论是1000x1000像素的图片,还是5000x5000像素的图片,CNN的参数都可以是一样的值。CNN极大的减少了parameter的个数,不会随着图片的像素数增加而增加,降低了overfitting。
符号总结(符号和维度顺序惯例):
- \(l\):表示CNN的层数是第\(l\)层,用上标\([l]\)标记哪一层的参数。
- \(f^{[l]}\):filter的大小,即filter矩阵的长或宽,一般长宽相等。
- \(p^{[l]}\):padding的大小
- \(s^{[l]}\):stride步长
- \(n_C^{[l]}\):输出的channel数,也是当前层filter的个数,下一层filter的channel数
- \(n_H^{[l]}\):图片矩阵的height
- \(n_W^{[l]}\):图片矩阵的width
对\([l]\)层来说:
- 输入维度是:\(n_H^{[l-1]} \times n_W^{[l-1]} \times n_C^{[l-1]}\)
- 输出维度是:\(n_H^{[l]} \times n_W^{[l]} \times n_C^{[l]}\)
- 单个filter的维度是:\(f^{[l]} \times f^{[l]} \times n_C^{[l-1]}\) (注意:本层filter的channel和上一层输出的channel一样)
- 所有filter(\(n_C^{[l-1]} \)个)组成当前layer的Weight:\(f^{[l]} \times f^{[l]} \times n_C^{[l-1]} \times n_C^{[l]} \)
- bias的维度是:\(1 \times 1 \times 1 \times n_C^{[l]}\)
- activations(\(a^{[l]}\))的维度和输出维度一样:\(n_H^{[l]} \times n_W^{[l]} \times n_C^{[l]}\)
- 对于batch gradient,考虑到样本数\(m\),则\(A^{[l]}\)的维度是\(m \times n_H^{[l]} \times n_W^{[l]} \times n_C^{[l]}\),编程实践上也采用这个顺序的维度。
根据之前的公式,有输出height、width和输入的关系如下:
\[n_H^{[l]} = \biggl\lfloor \frac{n_H^{[l-1]}+2p^{[l]}-f^{[l]}}{s^{[l]}}+1 \biggr\rfloor\] \[n_W^{[l]} = \biggl\lfloor \frac{n_W^{[l-1]}+2p^{[l]}-f^{[l]}}{s^{[l]}}+1 \biggr\rfloor\]1.8- Simple Convolutional Network Example
下图是一个简单CNN网络的例子:
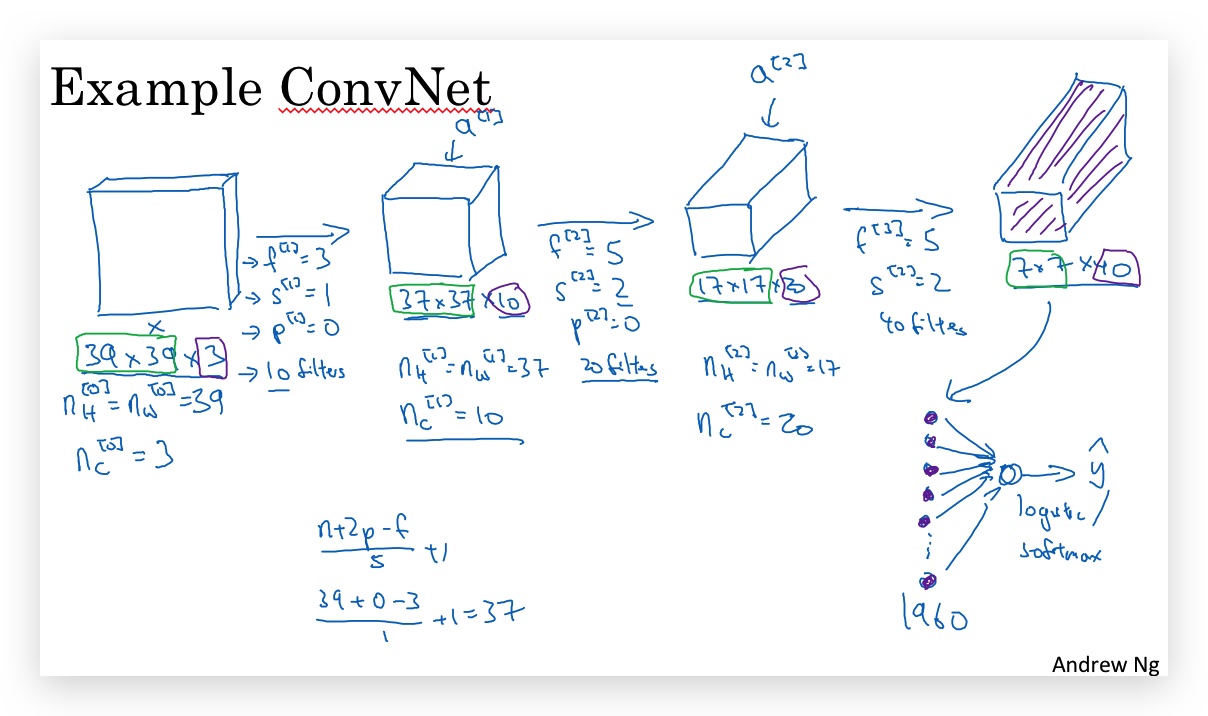
- 输入图片是39x39x3的维度。
- 最后的输出volume,unroll成一个vector,再通过logistic或softmax函数处理,实现分类。
- 一般而言,图片的height \(n_H^{[l]}\) 和width \(n_W^{[l]}\)随着层数的增加逐渐降低,但channel \(n_C^{[l]}\)逐渐增加。
Type of layer in a converlutional netwrok(ConvNet):
- Convolution (CONV)
- Pooling (POOL)
- Fully connected (FC)
1.9- Pooling Layers
- 除了卷积层(convolutional layers)外,卷积网络(ConvNets)还经常用池化层(pooling layers),主要好处是:
- 降低表示的大小,加快计算速度。
- 提高feature的鲁棒性。
pooling可分为max pooling和average pooling。
- Max pooling
下图是max pooling的示意图:
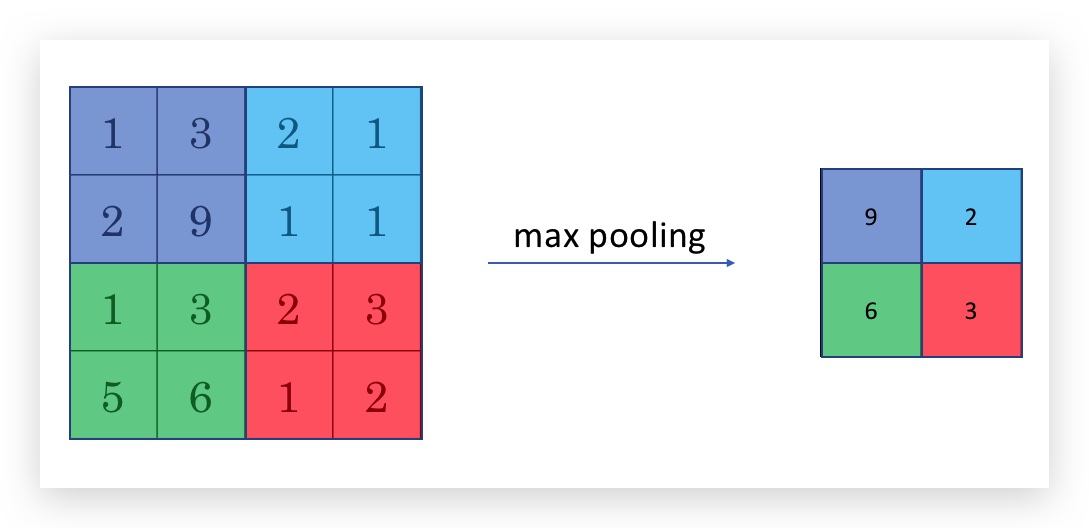
Max pooling的过程是,将原矩阵分成若干个分区(如上图四种颜色标记),每个分区内选择最大值,代表这个分区,组成一个新的矩阵。 上面的例子的作用结果(尤其是矩阵大小),也相当于一个作用了一个卷积filter,其大小是2x2,stride为2的。即:\(f=2\),\(s=2\),之前推导的filter大小公式也适用。因此max pooling也用\(f\)和\(s\)等作为其参数,但需要注意,对max pooling而言,这些参数是超参。
与卷积相比,max pooling并没有一个filter,或者说这个filter是一个全1矩阵,和重叠的矩阵元素相乘,然后取元素最大值,从这点看和卷积操作也是统一的。
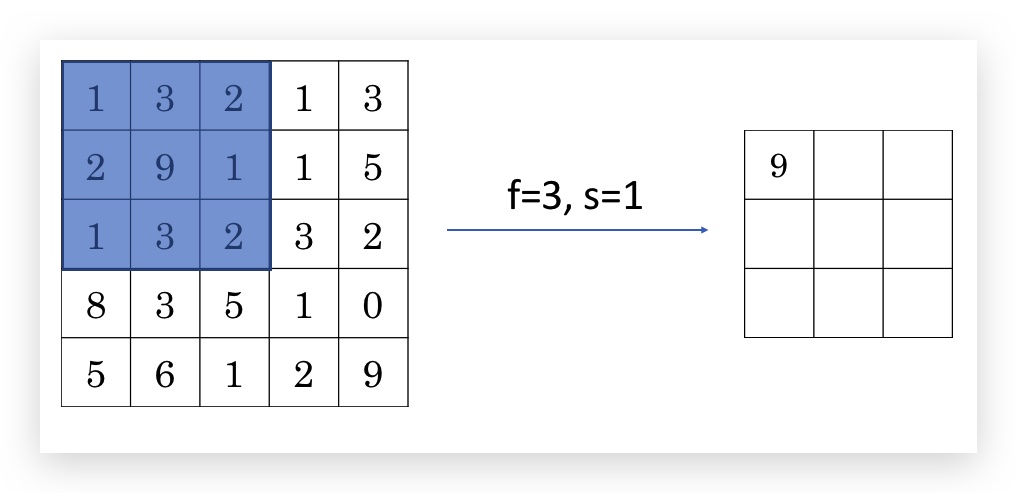
下图是一个f=3, s=1的max pooling例子:
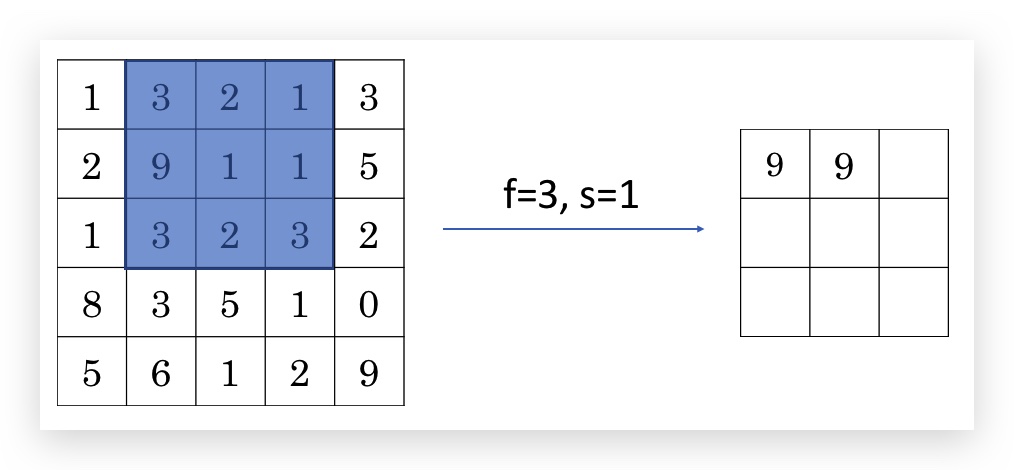
类似的,max pooling也是支持channel的,但与卷积不同,输出的channel和输入的channel数目是一样的(卷积输出channel总是一层,卷积相当于计算后的channel做了叠加,max pooling的channel之间互相独立)。
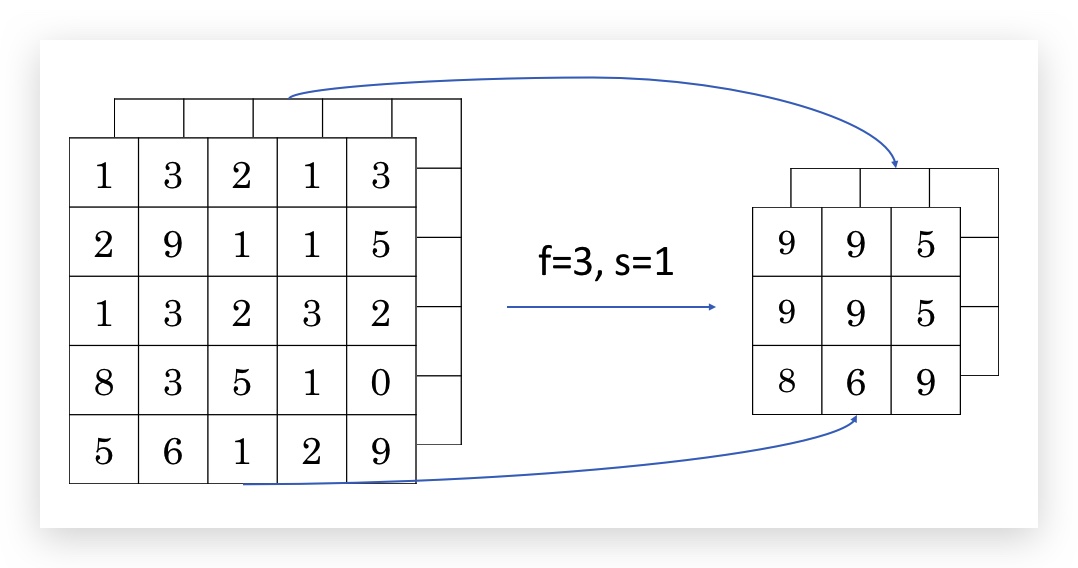
关于max pooling的直觉解释: 元素较大的值,可能是卷积过程中提取到的某些特征(比如边界),而max pooling则在压缩了矩阵大小的情况下,保留每个分区内最大的输出,即保留了提取的特征。但理论上还没有证明max pooling的原理,max pooling应用的原因是在实践中效果很好。
- Average pooling
与max pooling的不同仅在于最后取的是分区内的平均值,而不是最大值。比如:
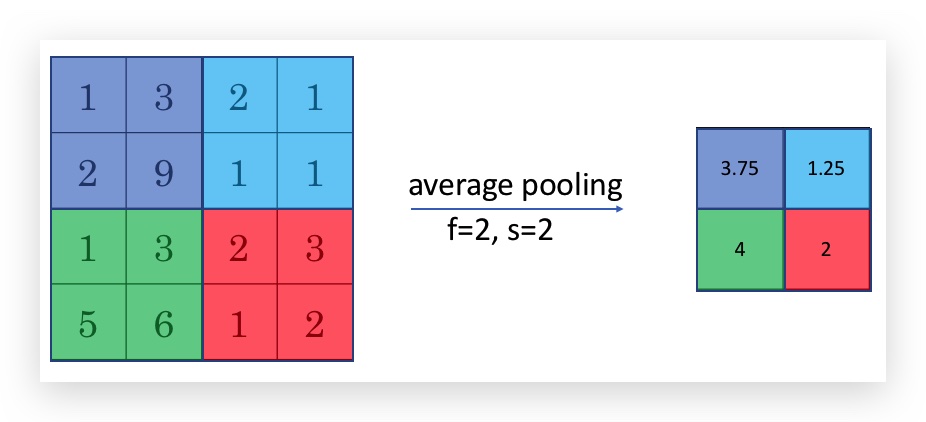
另外,Average pooling不如max pooling那么常用。
- pooling总结:
- 超参:
- f:filter size(通常选择f=2,s=2,实现对一张图片的shrink,长宽都shrink了一半)
- s:stride
- 选择max还是average pooling
- p:padding,几乎不会用到(因为pooling本身就是一个shrink的过程),或设置为0. * pooling没有需要学习的参数,只有超参。
1.10- CNN Example
前面已经了解了CNN需要的模块,下面通过一个例子介绍CNN网络:LeNet-5架构(与原论文略有修改),用来识别数字。 LeNet-5原版可参考论文:http://yann.lecun.com/exdb/publis/pdf/lecun-98.pdf
LeNet-5架构如下:
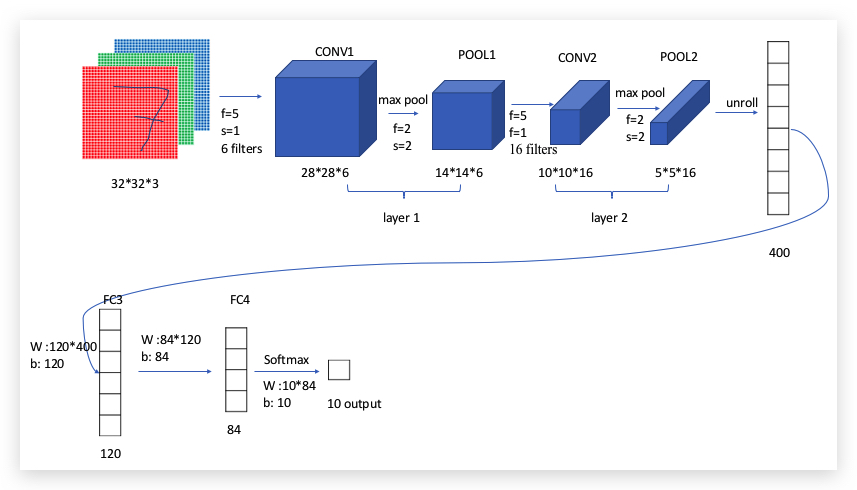
- 通常Conv Layer和Pooling Layer合在一起算一个layer,因为pooling layer并没有参数训练
- 常见的结构:Conv ==> Pool ==> Conv ==> Pool ==> FC ==> FC ==> softmax
- 最终还会用FC层(全连接层),与一般NN的处理一样;并在输出层,应用softmax得到10个数字的概率。
- 在整个网络中,Height和Width是逐渐递减的,但channel和filter是递增的。
- 关于CNN如何选择超参:可以参考论文的经验。
整个例子的参数个数如下:
| Activation shape | Activation Size | #parameters | |
|---|---|---|---|
| Input: | (32, 32, 3) | 3072 | 0 |
| CONV1(f=5, s=1) | (28, 28, 6) | 4704 | 156 (=5*5*6+6) |
| POOL1 | (14, 14, 6) | 1176 | 0 |
| CONV2(f=5, s=1) | (10, 10, 16) | 1600 | 416 (=5*5*16+16) |
| POOL2 | (5, 5, 16) | 400 | 0 |
| FC3 | (120, 1) | 120 | 48120 (=120*400+120) |
| FC4 | (84, 1) | 84 | 10164 (=84*120+84) |
| Softmax | (10, 1) | 10 | 850 (=10*84+10) |
- pooling layer没有参数
- CONV layer的参数相比FC的parameter会少很多。
- activation size递减 (activation size总是和feature相等的,feature一直在缩减)
1.11- Why Convolutions?
CONV Layer相比一般神经网络的全连接层的优势:
-
参数共享(parameter sharing) 以上一节的例子为例,如果在第一层就用FC的话,参数可达4704*3070 + 4704个,这个数字已经膨胀到了1400万,而这还仅是训练一个只有32*32像素的小图片。 而CONV Layer只有156个参数。 参数共享为什么可行呢?一个feature检测器,即filter(比如垂直边界检测)在图片的一个地方适用,也很可能在图片的其他地方适用(我的理解:在这一点上很像transfering learning或multi-task learning)。这种共享不仅在底层feature有用,也在高层feature有用(比如检测眼睛)。
-
稀疏连接(sparsity of connections) 稀疏连接是指,输出中的每个单元仅和输入的一个小分区相关,比如输出的左上角的像素仅仅由输入左上角的9个像素决定(假设filter大小是3*3),而其他输入都不会影响。
基于上述的特点,CNN网络可以使用较少的参数,使用较少的训练数据,并且不容易overfitting。 另外CNN也特别适合捕捉平移不变形(Translation Invariance)。
附:直观展示CNN网络:http://scs.ryerson.ca/~aharley/vis/
-------------------------
本文采用 知识共享署名 4.0 国际许可协议(CC-BY 4.0)进行许可。转载请注明来源:https://imshuai.com/deeplearning-ai-notes-course4-week1 欢迎指正或在下方评论。