本周介绍了CNN的两个特殊应用：人脸识别、图片风格转移。前者，着重于使用Siamese Network通过triplet loss或binary Classification解决了人脸识别的One Shot Learning问题。后者，通过构建Content Cost和Style Cost实现风格转移。另外还将卷积推广到了1D和3D数据。

1- Face Recognition

1.1- What is face recognition?

与人脸识别（Face Recognition）相关的还有活体检测（Liveness Detection）问题，在这里仅讨论前者。

Face verification（人脸验证） vs. face recognition（人脸识别）

  • 人脸验证：一对一的问题，给定一张人脸图片和一个身份信息，验证图片和身份是否匹配
  • 人脸识别：要比人脸验证困难，一对多问题。对一个K个人的数据库，给定一张图片，判断这张图片是K个人种的哪一个（或不是K中的任何一个）

1.2- One Shot Learning

人脸识别的一个挑战是One Shot Learning，即人脸识别程序需要仅根据某人的一张图片去识别这个人。

人脸识别的可能的方法：假如有4个人要识别，则构建一个ConvNet，最后一层softmax输出4个维度，分别代表4个人。但由于每个人只有一张人脸图片，训练效果很差。并且如果增加了新人，还要修改softmax的输出是5个维度，重新训练网络，显然这是不现实的。

换个角度，让算法不是训练识别一个具体的人，而是训练一个相似性函数（similarity function）：d(img1, img2)，代表两张图片的差异度。并设置一个阈值\(\tau\)，如果\(d(img1, img2) \le \tau \)，则认定为两张图片是同一个人，否则是不同的人。这就解决了one shot learning 问题。

1.3- Siamese Network

实现相似性函数d的一个方法是Siamese Network。

将人脸图片\(x^{(1)}\)经过ConvNet的输出，最后不经过softmax，而是使用全连接层，得到的向量\(f(x^{(1)})\)，将其看做输入图片\(x^{(1)}\)的编码（encoding）：

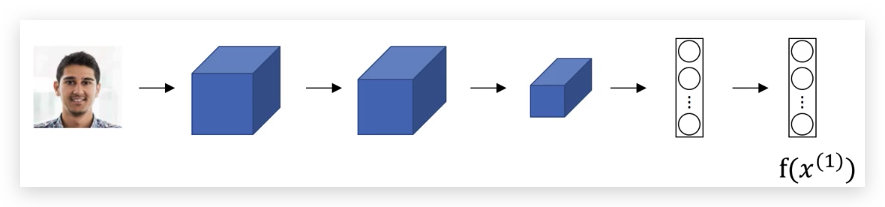
Xnip2018-07-16_21-54-22

在计算两张人脸图片的\(x^{(1)}\)和\(x^{(2)}\)似性函数时，先使用相同的ConvNet分别得到其编码\(f(x^{(1)})\)和\(f(x^{(2)})\)，将差异度的计算转化为对编码\(f\)的计算（两个向量之差的L2范数）：

\[d(x^{(1)}, x^{(2)}) = ||f(x^{(1)}) - f(x^{(2)})||^2_2\]

这种方法叫做：Siamese Network

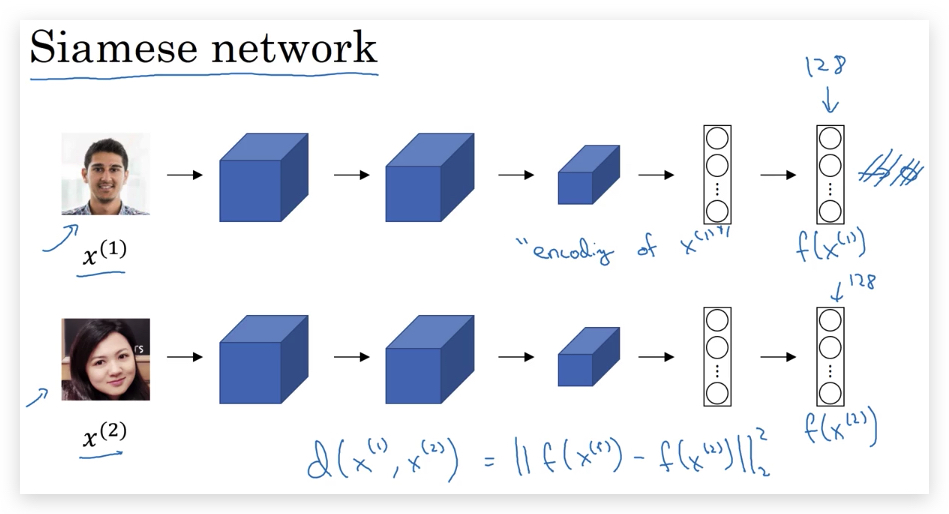
Xnip2018-07-16_21-48-22

paper参考：Taigman et al., 2014, DeepFace closing the gap to human level performance

训练上述Siamese Network的目标是：

  • NN网络的参数决定了编码\(f(x^{(i)})\)
  • 学习这样的参数，使得如果\(x^{(i)}\)和\(x^{(j)}\)表示同一个人，则\(   f(x^{(i)}) - f(x^{(j)})   ^2_2\)的值非常小。如果表示不同的人，则\(   f(x^{(i)}) - f(x^{(j)})   ^2_2\)非常大。

1.4- Triplet Loss

为了达到上面训练Siamese Network的目标，我们需要定义Loss Function，有一种方法就是Triplet Loss。

为此，对每一个人脸需要准备三种训练数据：

  • Anchor
  • Positive
  • Negative

其中Anchor和Positive是同一个人的人脸图片，而Negative和Anchor是不同人的人脸图片。

训练的目标是让\(d(A,P) \le d(A,N)\) （A代表Anchor，P代表Positive，N代表Negative），即：

\[(||f(x^{(A)}) - f(x^{(P)})||^2_2 \le ||f(x^{(A)}) - f(x^{(N)})||^2_2\]

或写成:

\[||f(x^{(A)}) - f(x^{(P)})||^2_2 - ||f(x^{(A)}) - f(x^{(N)})||^2_2 \le 0\]

很容看到，对上面的目标函数有一个平凡解：即\(f(x)=0\)，显然这是不符合要求的，所以，上式会增加一个很小的正数\(\alpha\)（称为margin），规避这种情况，即：

\[||f(x^{(A)}) - f(x^{(P)})||^2_2 - ||f(x^{(A)}) - f(x^{(N)})||^2_2 + \alpha \le 0\]

最后，我们整理如下的Loss Function：

\[L(A,P,N) = max(||f(x^{(A)}) - f(x^{(P)})||^2_2 - ||f(x^{(A)}) - f(x^{(N)})||^2_2 + \alpha, 0)\]

由于每组训练数据都需要上述三种图片（A,P,N）组成，所以上面的Loss Function称之为Triplet Loss。

上式中，使用了max和0比较，即只要达到区分度即可，并不过分追求AP和AN的差异。

对大小为\(m\)的Training Data，Cost Function则为：

\[J = \sum^m_{i=1}L(A^{(i)}, P^{(i)}, N^{(i)})\]

可以使用Gradient Descent对上述\(J\)优化。

在训练阶段，需要一个人的多张照片，而在预测阶段，只需要一张照片即可。本质上one-shot learning并不是learning的过程，而是预测的过程。算法学习的并不是对若干人脸的直接分类，而是通过Triplet Loss学习对不同人的脸能有效区分，相同人的脸有效接近的编码\(f\)。这个编码\(f\)就是某个ConvNet。

在训练数据选择Triplet的需要注意，如果随机的选择A/P/N图片组，由于A和N本身很可能差异很大的，很容易满足\(d(A,P) + \alpha \le d(A,N)\)，导致训练结果不够鲁棒；实践中，会选择训练起来比较困难的A/P/N图片组。

paper参考：Schroff et al., 2015, FaceNet: A unified embedding for face recognition and clustering

另外，当前商业化的人脸识别，基于的数据量在百万级以上，甚至到达千万、亿的级别。这些数据获取并不容易，训练量也很大。幸运的是，有一些已在大数据级上训练的参数开源了，可以在此基础上实现。

1.5- Face Verification and Binary Classification

除了triplet loss，还有一种比较有效的方法训练Siamese Network的参数：Binary Classification。

与Triplet Loss不同，每个训练样本是两张人脸图片，输入到一个Siamese Network（上下两个网络的参数一样），分别得到两张图片的编码\(f(x^{(i)})\)和\(f(x^{(j)})\)，最后将两个编码通过sigmoid做一个Binary Classification，同一个人输出1，否则输出0。

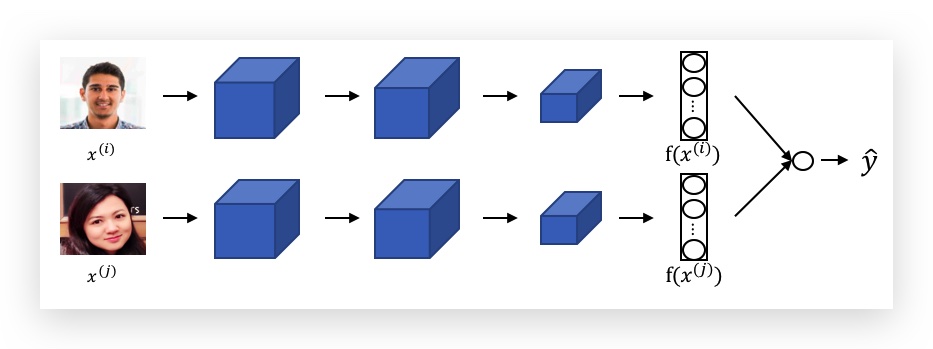
Xnip2018-07-17_08-42-51

其中最后的sigmoid形式可以是：

\[\hat y = \sigma (\sum^K_{k=1}w_k|f(x^{(i)})\_k - f(x^{(j)})\_k)| + b)\]

即将两个编码的元素级之差的绝对值作为激活函数的输入。激活函数的输入也可以使用\(\chi\)相似度，即：

\[\hat y = \sigma (\sum^K_{k=1}w_k \frac{(f(x^{(i)})_k - f(x^{(j)})_k)^2}{f(x^{(i)})_k + f(x^{(j)})_k} + b)\]

预测阶段的优化：无论是Triplet Loss还是Binary Classification，预测阶段都会用一张待验证人脸与系统存储的人脸进行比对，由于系统存储的人脸是固定的，每次输入到Siamese Network计算其编码结果不变，因此可以直接将其编码缓存起来，降低计算量。甚至系统内也不用存储原始图片，只存储图片对应的编码向量即可。

paper参考：Taigman et. al., 2014. DeepFace closing the gap to human level performance

2- Neural Style Transfer

2.1- What is neural style transfer?

Neural Stlye Transfer，直观上就是将一种图片的风格应用到另一张内容图片上，比如：

Xnip2018-07-17_08-59-57

整个过程涉及三张图片，Style图片提供风格，Content图片提供内容，Generated Image是生成的图片。接下来将用S、C、G分别代表三种图片。

2.2- What are deep ConvNets learning?

为了实现Style Transfer，首先需要了解神经网络的每一层都在做什么。本节通过可视化的方法，研究ConvNet的每一层都在做什么。

假如有如下的ConvNet：

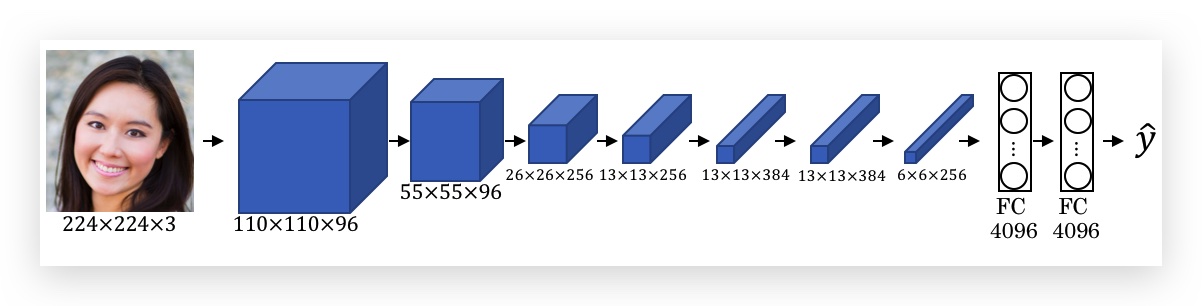
Xnip2018-07-17_10-42-58

可视化思路是，对某一层layer中选择一个unit，遍历所有训练样本，选择使该unit的激活函数最大的9块图像区域，使用这9个图像块作为这个unit的可视化；以此类推可视化所有unit。使得激活函数最大，说明这个unit对某个特征敏感，是其捕捉的特征。

下图是每一层选择了9个unit做可视化示例（每个unit用9个激活函数最大的图像块代表，每个layer选择了9个unit）：

Xnip2018-07-17_10-59-55

可以看到：

  • 浅层网络识别了图像的边缘、纹理、颜色的过渡等较简单的低层次特征；
  • 深层的unit，其识别的区域较大，特性更具体，比如狗的脸、汽车的轮子等。
  • 观察每个unit的9个色块，很容易发现具有相似的共性特性，即该unit识别的特征。

paper参考：Zeiler and Fergus., 2013, Visualizing and understanding convolutional networks

2.3- Cost Function

为了构建Neural Style Transfer系统，我们需要为生成图片定义Cost Function（这也是机器学习的套路了）。通过最小化Cost Function，可以生成目标图片G。

显然目标图片需要兼具内容图片的内容和风格图片的风格特征，因此Cost Function由两部分组成：内容图片C与G的Content Cost Function，以及风格图片S与G的Content Cost Function，即：

\[J(G) = \alpha \cdot J_{content}(C, G) + \beta \cdot J_{style}(S, G)\]

其中\( \alpha\)和\( \alpha\)是控制两部分权重的超参。特别注意：G就是要训练的参数。

算法过程：

  • 随机生成G的每个像素点。（即参数初始化）
  • 使用Gradient Descent最小化Cost Function \(J(G)\)，在这个过程中G会慢慢的生成，就像这样：

Xnip2018-07-17_12-21-21

需要注意的是，普通cost function优化的结果是网络上的参数，而Neural Style Transfer在cost function上优化的结果是：G的每一个像素，而此cost function也并没有对应什么神经网络。

下面具体介绍如何表示\( J_{content}(C, G)\)和\(J_{style}(S, G)\)

2.4- Content Cost Function

计算Content Cost Function，即\( J_{content}(C, G)\)的方法：

  • 使用一个训练好的ConvNet，如VGG网络。（这个ConvNet的训练不属于Style Transfer的范围）
  • 使用ConvNet的某一个隐藏层\(l\)计算Content Cost。隐藏层\(l\)的选择，通常是网络中处于中间的隐藏层。如果太浅，则隐藏层和原始图片看起来差不多，如果太深，则太过于具体。
  • 图片C和G的Cost Function可表示为： \(J_{content}(C, G) = \frac{1}{2}||(a^{(C)[l]} - a^{(G)[l]})||^2\) 其中，\(a^{(C)[l]}\)和\(a^{(G)[l]}\)分别为C和G在\(l\)层的激活函数。

隐藏层激活函数\(a^{(C)[l]}\)和\(a^{(G)[l]}\)越接近，\(J_{content}(C, G)\)越小，则暗示C和G图片的内容越接近。（疑问：为什么激活函数的相近代表了图片内容的接近？）

2.5- Style Cost Function

一个张图片的style是什么含义？ 如果用\(l\)层的激活函数来度量style，我们定义style为不同channel之间激活函数的相关性（Correlation）。

为什么不同channel之间的相关性可以代表style呢？根据前面章节所述，每个channel会学习一种特征，比如颜色、纹理等。这些特征的相关性，表示这些特征是否会倾向于同时出现。

下图表示每个channel学习到不同的特征，比如红色的channel学习到了垂直的纹理，黄色的channel学习到了橘黄色：

Xnip2018-07-18_09-36-59

直观的感觉一下梵高的星夜，它的style是什么？是蓝色和黄色和黑色混杂，有搅动感的漩涡。如果神经网络的多个channel识别了这个特征，那么这些channel的激活函数相关性一定很大。

channel的相关性，表名了某些特征多大机会同时出现或不同时出现。style就是某些特征的混杂。

下面是正式的数学表示：

  1. 首先定义两个符号：
    • 用\(a^{[l]}_{i,j,k}\) 表示第\(l\)层在volume中处于\((i,j,k)\)位置的激活函数。其中\(i\)是width（即在\(n^{[l]}_W\)的维度上），\(j\)是Height（即在即在\(n^{[l]}_H\)的维度上），而\(k\)是channel（即在\(n^{[l]}_C\)的维度上）。
    • 用\(G^{[l]}\)表示style matrix，实际上就是\(l\)层所有channel组成的相关矩阵，所以其维度是\(n^{[l]}_C \times n^{[l]}_C\)。而\(G^{[l]}_{kk’}\)即第\((k,k’)\)个元素，代表第\(k\)个channel和第\(k’\)个channel的相关性。style matrix之所以用大写字母G表示style matrix，是因为在数学上，它称之为gram matrix。

  2. Style matrix \(G^{[l]}_{kk’}\)的计算如下：

    \[G^{[l]}\_{kk'} = \sum^{n^{[l]}\_H}\_{i=1} \sum^{n^{[l]}\_W}\_{j=1} a^{[l]}\_{ijk} a^{[l]}\_{ijk'}\]

    直观的来说，就是第\(k\)个channel和第\(k’\)个channel这两个矩阵的元素级乘积的和。可以理解成向量的内积，而内积反应的就是相关性。

    对于style matrix，我们需要分别在图片S和图片G上计算，因此再增加一个上标，分别表示S和G的style matrix的计算：

    \[G^{[l]\(S)}\_{kk'} = \sum^{n^{[l]}\_H}\_{i=1} \sum^{n^{[l]}\_W}\_{j=1} a^{[l]\(S)}\_{ijk} a^{[l]\(S)}\_{ijk'}\] \[G^{[l]\(G)}\_{kk'} = \sum^{n^{[l]}\_H}\_{i=1} \sum^{n^{[l]}\_W}\_{j=1} a^{[l]\(G)}\_{ijk} a^{[l]\(G)}\_{ijk'}\]
  3. 有了S和G的style matrix，就可以定义style的cost function了，即两个style的差异：
\[J^{[l]}\_{style}(S, G) = \frac{1}{(2n^{[l]}\_Hn^{[l]}\_Wn^{[l]}\_C)^2} || G^{[l]\(S)} - G^{[l]\(G)}||^2_F\]

即两个style matrix元素级相减后，再将元素做平方和（下标F表示Frobenius norm，在之前的课程有提到：L2 Regularization）展开后即：

\[J^{[l]}\_{style}(S, G) = \frac{1}{(2n^{[l]}\_Hn^{[l]}\_Wn^{[l]}\_C)^2} \sum_k^{n^{[l]}\_C} \sum_{k'}^{n^{[l]}\_C}(G^{[l]\(S)}\_{kk'} - G^{[l]\(G)}\_{kk'})^2\]
  1. \(J^{[l]}_{style}(S, G)\)只是第\(l\)层的cost function，所有层的cost function之和组成了全部的cost function：
\[J_{style}(S, G) = \sum_l^L \lambda^{[l]} J^{[l]}\_{style}(S, G)\]

其中\(\lambda^{[l]}\)是对每层cost function的权重，也是一个超参。

通过捕捉不同类型的特征以及这些特征同时出现的程度，Style matrix 定义了一张图片的style。另外，与计算Content Cost只用某一个隐藏层不同，计算Style Cost使用了所有隐藏层。

2.6- 1D and 3D Generalizations

之前，都是针对图片使用卷积神经网络，数据都2D的，因此都是2D卷积。统一，卷积也可以推广到1D和3D数据。

  1. 1D卷积

比如心电图（EKG, Electrocardiography）就是1D数据，使用1D的filter做卷积运算。与2D类似，1D的filter在心电图数据上从左到右滑动。14维的数据应用5维的filter（stride是1），将输出10维的数据。输入数据也可以是多个channel，此时filter保持数量一致的channel；应用多个filter，则输出就是多个channel。

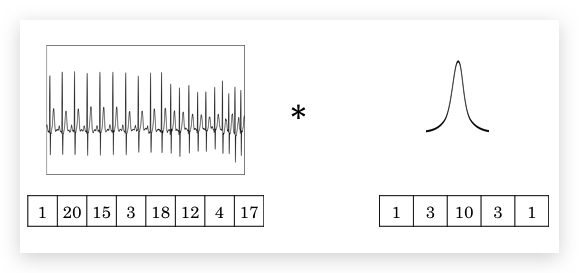
Xnip2018-07-19_20-22-28

1D卷积网络，可以应用于1D数据，但事实上更常用的是递归神经网网络（RNN, Recurrent Neural Network）。

  1. 3D卷积

比如CT数据就是3D数据，对人体进行若干层的切片扫描，每层是一张2D的图片，所有图片组成3D数据。

此时的输入数据和fitler都是3D的（注意，这里的3D和之前因多个channel画成的3D不一样）

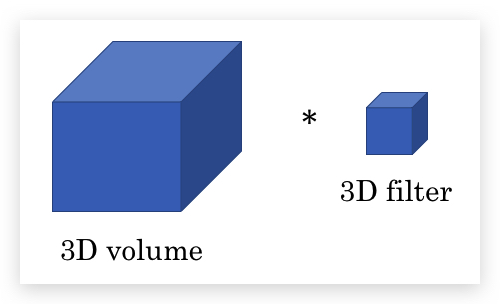
Xnip2018-07-19_20-29-35

比如一个14x14x14的输入数据，使用5x5x5的filter（stride是1），输出数据是10x10x10的数据。同样输入数据也可以是多个channel，使用多个filter。

-------------------------

本文采用 知识共享署名 4.0 国际许可协议（CC-BY 4.0）进行许可。转载请注明来源：https://imshuai.com/deeplearning-ai-notes-course4-week4 欢迎指正或在下方评论。