1- Optimization algorithms

应用Machine learning是一项非常经验性（empirical）的过程，需要训练很多模型，然后找出效果最好的。因此，训练的速度够快是至关重要的。

本周课程介绍几种加快Gradient descent的算法： * mini-batch * momentum * RMSprop * Adam * Learning rate decay

另外，在最后说明了梯度下降的主要问题不是local optima问题，而是plateaus问题。

1-1 Mini-batch gradient descent

1. Vectorization本身已经很大程度提升了gradient descent的速度，但之前介绍的是最基本的gradient descent算法（即batch gradient descent） 要遍历所有m个数据样本才会做一次梯度下降 。随着m的增大，这个过程会很慢，一次梯度下降的成本变得很大。
2. mini-batch gradient descent即针对上述问题，每次只使用少量的样本（即min-batch大小）去做迭代，计算梯度并更新参数。由于不少全量样本，计算的梯度不一定很准，即存在抖动（后面会通过其他算法解决抖动），但速度很快 。因此，同样是遍历了m个样本，min-batch算法可以拆分成多个批次，做到更多次梯度下降，达到更快的下降速度。
3. 引入标记：使用上标{i}表示拆分出的第i个批次。比如 \(X^{\{i\}}\) 表示第i个批次组成的数据集。如果一个批次的大小是1000，则每个批次的数据集\(X^{\{i\}}\) 的shape都是\((n_x, 1000)\) ， Y的shape是(1, 1000)（不考虑最后一个批次零头的情况）。
4. mini-batch算法很简单：
   • 先确定分多个batch，假如总的数据集大小是500万，分成5000个批去做，那么每个批处理1000个数据集。循环5000个批次：
   • 每个批次取出对应批次的1000条数据，在一个批次内，和传统的gradient descent没有差别，唯一就是输入的数据集不是全集，而一个批次。
5. epoch：当所有批次都循环完成了，即全部m个数据集都参与过了计算，这叫一个epoch。整个算法在epoch层还会做循环，迭代很多次epoch。
6. 在大数据下，基本上必然要采用min-batch gradient descent。
7. 相比而言，mini-batch gradient descent的迭代过程会比较震荡。
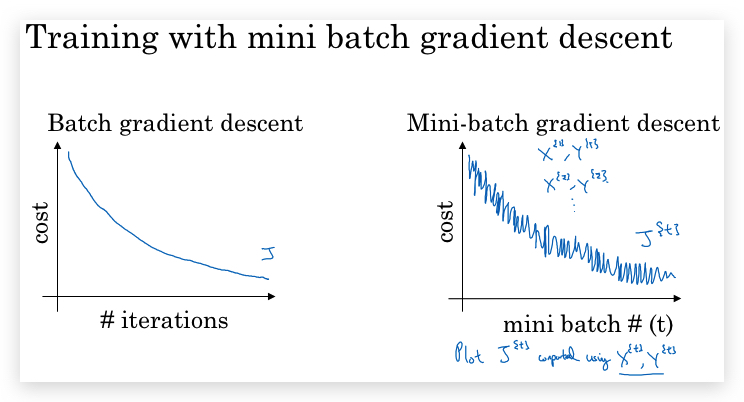
8. 不同mini-batch size（批次大小，即一个批次包含的样本数）的区别：
   • gradient descent可以认为是mini-batch size是m的mini-batch gradient descent。噪声较小，但一次下降的计算速度太慢。
   • 如果mini-batch size = 1，则每次只用一个样本做梯度下降，则变成 stochastic gradient descent （随机梯度下降）。噪声太大，且失去了vectorization加速。
   • mini-batch和stochastic都存在噪声问题，且在local optima附近会徘徊。但设置合适大小的mini-batch size，噪声和徘徊问题可接受的范围内。
9. 如何选择mini-batch size（这是一个hyperparameter）：
   • 小数据量，比如总的样本只有几千个，完全可以直接用batch gradient descent
   • 大数量，mini-batch size倾向于选择2^n个，比如64, 128, 256等
   • mini-batch 与CPU/GPU memory的内存容量。

1-2 Exponentially weighted averages

Exponentially weighted averages（指数加权平均），在统计学也称作Exponentially weighted moving averages（指数加权滑动平均）

Exponentially weighted averages概念举例：

下图蓝色点是伦敦某段时间每日温度值\(\theta_t\)，而红色是加权平均后的\(v_t\)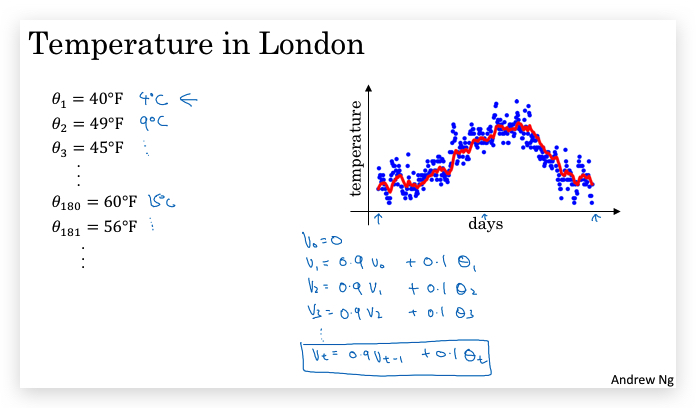，  具体的加权平均方法是：每天的温度值加权值\(v_t\)设置为前一天的温度加权值\(v{t-1}\)和当天的温度实际值\(\theta_{t}\)做加权平均： \(v_t = \beta v_{t-1} + (1-\beta) \theta_{t}\)

参数β的影响是，β越大，则：

1. 曲线越平滑
2. 曲线会比实际值向右偏移

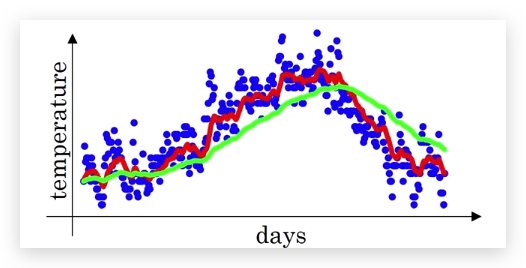
比如图中，绿色的β就比红色的β大。β越大代表历史数据的权重越大，稳定性越好，同样也更迟钝。

如何理解Exponentially weighted average

假如β=0.9，每个v的计算如下： \(v_{100} = 0.9v_{99} + 0.1 \theta_{100}\) \(v_{99} = 0.9v_{98} + 0.1 \theta_{99}\) \(v_{98} = 0.9v_{97} + 0.1 \theta_{98}\)

递归展开\(v_{100}\)，得到如下： \(v_{100} = 0.1 \theta_{100} + 0.1 * 0.9 \theta_{99} + 0.1 * {(0.9)}^2 \theta_{98} + ...\)

一般的： \(v_t = \sum\limits_{i = 1}^{t} (1-\beta)\beta^{t-i}\theta_i\)

另有无穷级数求和： \(\sum\limits_{t = 1}^{n} (1-\beta)\beta^{t} = 1\)

因此可以近似的认为所有项的系数之和正好为100%。

即，\(v_t\)是对t日之前所有的实际温度的加权平均，而每个\(\theta_t\)给予的权重是\(\beta^{t-i}\)，这个权重是指数递减的，越早的数据权重越小。这就是Exponentially weighted average名称的来源。

另外，有极限： \(\lim_{\varepsilon \to 0} (1-\varepsilon)^{\frac{1}{\varepsilon}} = \frac{1}{e}\)

因此当\(\varepsilon\)足够小的时候，认为： \((1-\varepsilon)^{\frac{1}{\varepsilon}} \approx \frac{1}{e}\)

当β取0.9的时候， \(\beta^{t} = 0.1^{10} = (1-0.1)^{\frac{1}{0.1}} \approx \frac{1}{e} \approx 0.35\) 即当β取0.9时，10天前的气温的权重就衰减到了只有0.35，如果将其忽略，则有

\(v_t\)近似的等于最近\(\frac{1}{1-\beta}\)天的温度加权平均值： \(v_t \approx avg(\frac{1}{1-\beta} days' temperature)\) 比如β=0.9，则近似相当于最近10天的温度加权均值。

一般的，可以认为，\(v_t\)近似的为前\(\frac{1}{(1-\beta)}\)天的加权平均值。

机器学习实践中的操作

1. 并不是无限制的计算所有历史值的加权平均，而是近似的做前\(\frac{1}{(1-\beta)}\)天的加权平均值。
2. 计算前\(\frac{1}{(1-\beta)}\)天的平均值，使用循环不断override的的方法，减少内存占用，只需一行代码： \(v := \beta v + (1 - \beta)\theta_t\)

Bias correction in exponentially weighted averages

由于计算\(v_1\)的时候，并没有历史值做加权，这个时候令其前一个加权值\(v_0 = 0\)，则会导致\(v_1 = (1-\beta)v_0 + \beta \theta_1 = \beta \theta_1\)，这个值会远小于\(\theta_1\)，进而\(v_2\)也会偏小，依次类推，在靠近前面的值会出现显著的小于实际值的情况：

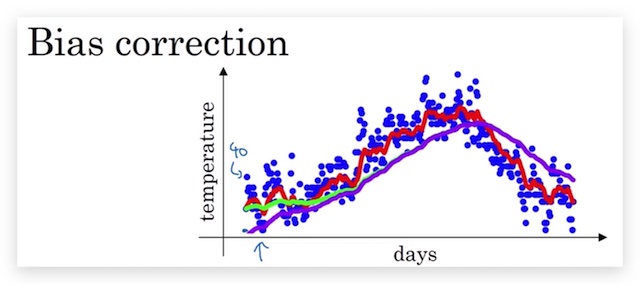
图中紫色部分的前端会明显的小于实际值。显然这是不合理的，需要修正。修正的方法是原来的计算值做如下操作： \(v_t:= \frac{v_t}{1-\beta^t}\)

合起来就是： \(v_t = \frac{\beta v_{t-1} + (1 - \beta)\theta_t}\)

在t较小的时候，\(1-\beta\ \approx 1-\beta^t\)，也就是加大了\(\theta_t\)本身的权重，但当t足够大的时候，这个修正微乎其微，因此只对前面的数据有实际影响。

即便如此，在真正的Machine Learning中，也并不做这种“没必要的”修正，因为在Machine Learning中看重的是很多次迭代后的结果，初期的偏差影响并不大。

1-3 Gradient descent with momentum

In one sentence, the basic idea is to compute an exponentially weighted average of your gradients, and then use that gradient to update your weights instead.

1. 问题背景：
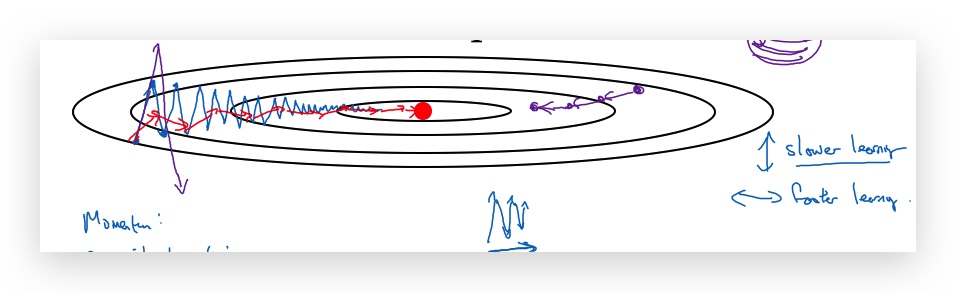
   • 某个方向（属性范围较小的，如上图蓝色曲线的垂直方向）出现震荡，会让梯度下降速度会变慢（Just slowly oscillate toward the minimum. And this up and down oscillations slows down gradient descent and prevents you from using a much larger learning rate.）
   • 然而，又不能通过加大learning rate解决，因为这样会在出现overshooting（如上图左边的紫色曲线）。
   • 因此，在不同的参数上，希望速度不一样，比如上图垂直方向希望慢一点（避免震荡），而水平方向希望快一点（加快到optima）。基于此就有了Gradient descent with momentum。
2. 应用exponentially weighted average
   • 与上面伦敦气温类似，这里将每轮迭代的梯度做exponentially weighted average处理
   • 每次梯度迭代（下面的式子省略标注参数所在的layer，另外\(v_{dW}\)和\(v_{dW}\)初始化为0）: \(v_{dW} := \beta v_{dW} + (1 - \beta) dW\) \(v_{db} := \beta v_{db} + (1 - \beta) db\) \(w=w - \alpha v_{dW}\) \(b=b - \alpha v_{db}\) 新的算法使用\(v_{dW}\)和\(v_{dW}\)代替了原始的梯度。这样，可以让gradient更平滑
   • 对于上图垂直方向，原来是会上下震荡，但引入了exponentially weighted average，相当于对前面的震荡进行了平均，结果就是上下震荡互相抵消了。而水平方向都是向右没有震荡，因此平均后还是向右。最终导致呈现上图红色的下降路线。
3. Intuition for momentum 可以将上面的图想象成一个碗，梯度下降就像一个小球往碗底滚，而β的作用就相当于摩擦力。
4. 引入了超参：β，实践中通常取0.9。
5. 通常并不像上面计算温度的时候需要做bias correction，因为对梯度下降来说迭代次数很多，初期的不准确影响并不大，如果β为0.9，大概10次就看不到bias了。
6. 另外，对于抑制mini-batch的震荡也有很好的效果： Because mini-batch gradient descent makes a parameter update after seeing just a subset of examples, the direction of the update has some variance, and so the path taken by mini-batch gradient descent will “oscillate” toward convergence. Using momentum can reduce these oscillations. 换个角度理解：在mini-batch中，引入之前迭代gradient做平均，相当于变相考虑了全部的数据集的特征。

但关于上图我有个疑问，理论上属性做过normalizing之后，应该是整个图形趋于圆形，而不是椭圆啊？ 这个问题后面想通了：对于单层网络，你可以对数据集X做normalizing，但对于隐藏层，它的输入是上一层的输出，而上一层的输出并没有做normalizing。后面的课程提到了这一点，其思想就是对每一层activation function的输出都做normalizing。

1-4 RMSprop

RMSprop (Root Mean Square Propagation，均方根传递)，与momentum一样，也是降低梯度的抖动。以上面的图为例，降低处置方向的下降速率，并提升水平方向的下降速率。

实际上是对梯度的平方进行exponentially weighted average，但这个结果并不承担梯度的作用（Gradient descent with momentum却是这样，计算的\(v_{dW}\)代替了\(dW\)去更新参数。），而是平抑不同大小梯度的更新速率。实际上 作用在α上的。

1. 算法： \(s_{dw} = \beta s_{dw} + (1 - \beta)(dw)^2\) \(s_{db} = \beta s_{db} + (1 - \beta)(db)^2\) \(w := w - \alpha \frac{dw}{\sqrt{s_{dw} + \varepsilon}}\) \(b := b - \alpha \frac{db}{\sqrt{s_{db} + \varepsilon}}\)

其中上式中分母中增加\(\varepsilon\)通常取一个很小的值，仅仅是为避免出现分母太小趋近于0导致计算失败的问题。

1. Intuition 垂直方向，比较陡，梯度比较大，但我们又希望它下降的慢。因此对梯度除以一个较大的值，所以用梯度的平方的平均来表示。让不同的参数拥有不同的learning rate。

从某种角度看，RMSprop会根据当前的梯度自动调整参数的learning rate，梯度大降低learning rate，梯度小的时候提高learning rate，从而一方面避免了震荡，另一方面避免在平坦的地方徘徊太久。

1-5 Adam optimization algorithm

简单的说，Adam（Adaptive Moment Estimation，自适应矩估计）就是momentum和RMSprop的结合。momentum负责平滑梯度，而RMSprop负责调解learning rate。

算法如下（以下都省略了layer）：

1. 引入的变量有：
   • \(v\) : 计算同momentum算法，将梯度进行指数加权平均
   • \(s\) : 计算同RMSprop，将梯度的平方进行指数加权平均
   • \(\beta_1\) : 计算\(v\)的加权参数
   • \(\beta_2\) : 计算\(s\)的加权参数

2. 在迭代前，初始化参数v和s \(v_{dW} = 0, s_{dW} = 0, v_{db} = 0, s_{db} = 0\)

3. 对第t次梯度下降的迭代 a. 首先计算dw和db的v和s \(v_{dW} = \beta_1 v_{dW} + (1 - \beta_1) dW\) \(s_{dW} = \beta_2 s_{dW} + (1 - \beta_2) (dW)^2\) \(v_{db} = \beta_1 v_{db} + (1 - \beta_1) db\) \(s_{db} = \beta_2 s_{db} + (1 - \beta_2) (db)^2\)

   b. 然后做修正

   \(v^{corrected}\_{dW} = \frac{v_{dW}}{1 - (\beta_1)^t}\) \(s^{corrected}\_{dW} = \frac{s_{dW}}{1 - (\beta_2)^t}\) \(v^{corrected}\_{db} = \frac{v_{db}}{1 - (\beta_1)^t}\) \(s^{corrected}\_{db} = \frac{s_{db}}{1 - (\beta_2)^t}\)

   c. 最后更新参数W和b

   \[W = W - \alpha \frac{v^{corrected}\_{dW}}{\sqrt{s^{corrected}\_{dW}} + \varepsilon}\] \[b = b - \alpha \frac{v^{corrected}\_{db}}{\sqrt{s^{corrected}\_{db}} + \varepsilon}\]

超参的选择： - \(\alpha\)：需要调优 - \(\beta_1\): 通常选择为0.9 - \(\beta_2\): 通常选择为0.999 - \(\varepsilon\): 一般不需要调优，选择一个小数，比如\(10^{-8}\)

1-6 Learning rate decay

为什么要做learning rate decay？ 较大的learning rate虽然在算法开始阶段会加快收敛速度，但在收敛接近到优化点的时候，算法会在优化点附近震荡，如下图：

如何做learning rate decay？ 思路很简单，就是引入一个函数，让α随着迭代（比如min-batch的epoch）递减。为此可以采用的decay函数有：

• 倒数： \(\alpha := \frac{1}{1 + decay\\_rate * epoch\\_num} \alpha\)

• 指数函数： \(\alpha := 0.95^{epoch\\_num} * \alpha\)

• 根号倒数 \(\alpha := \frac{k}{\sqrt{epoch\_num}} * \alpha\)

甚至手工调节。

看到这里，我不禁想起来Andrew Ng在Machine Learning中提到的，learning rate不需要根据迭代去调整，因为越靠近optima，梯度本身就变小了，所有learning rate无需调节小。但引用到deep learning中的mini-batch情况，显然就不适合了。

1-10 The problem of local optima

直觉上，人们认为梯度下降的主要问题是收敛到local optima，如下图：

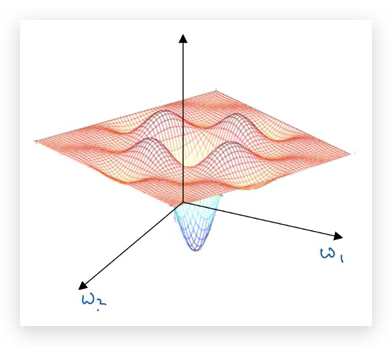
长期以来，这也是人们“直觉的误解”，但在高维空间里，其实local optima并不常见。原因就是在高维空间，所有维度同时得到同方向倒数（都是凹函数）为0的概率极低。更常见的情况是收敛到了鞍点（saddle），即某些维度取的是最小值，某些取的是最小值。

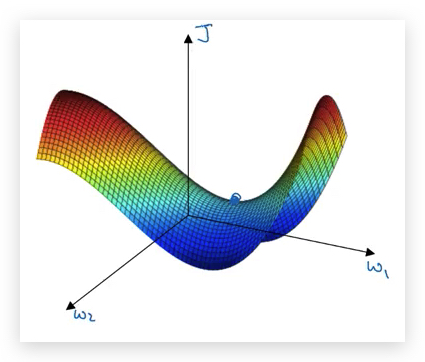
所有，担心收敛到local optima，真是人们想多了，实际上并没有想象的那么多local optima。在高维空间，几乎不太可能被困在一个local optima，这是一个好消息。

令人意外的是，这样一个误解，竟然在最近不久才被人们认识到。这部分可以参考我找的资料：https://www.zhihu.com/question/68109802

但梯度下降的真正挑战是高原问题（Problem of plateaus），即在广阔的高原上，梯度下降算法下降太慢。而Adam算法正好可以解决这个问题，在该加速的时候加速。

-------------------------

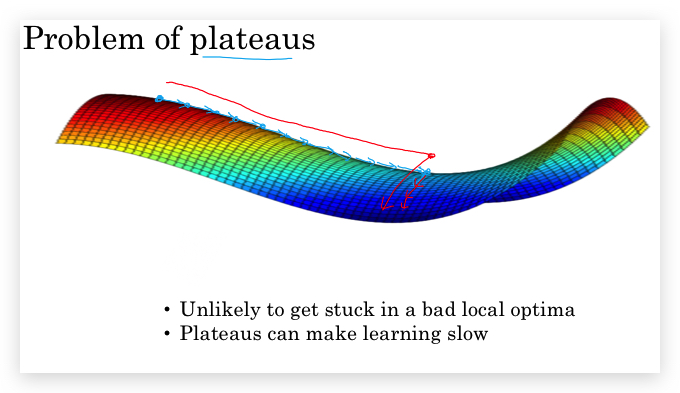
本文采用 知识共享署名 4.0 国际许可协议（CC-BY 4.0）进行许可。转载请注明来源：https://imshuai.com/deeplearning-ai-notes-course2-week2 欢迎指正或在下方评论。